Résumé de Cours de Sup et Spé T.S.I.
Troisième Partie : Géométrie
34 Coniques
Sous-sections
Une conique, éventuellement dégénérée, est une courbe plane ayant pour équation cartésienne 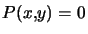 avec
avec 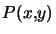 un polynôme du second degré.
un polynôme du second degré.
C'est : 
Les éléments de l'ellipse sont précisés figure ci-dessous.
![\includegraphics[width=6in]{ellipse}](img1175.png)
C'est : 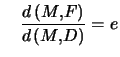 , avec
, avec 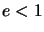
On a : 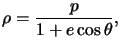 un des foyers
un des foyers  étant à l'origine
étant à l'origine
 est le paramètre de l'ellipse, distance du foyer à la directrice correspondante,
est le paramètre de l'ellipse, distance du foyer à la directrice correspondante,  est l'excentricité
est l'excentricité - l'axe focal est

- On trouve les autres paramètres en écrivant
 qui donne
qui donne 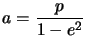
C'est : 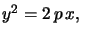 avec
avec 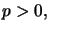 le paramètre
le paramètre
 est le sommet et
est le sommet et  l'axe de symétrie
l'axe de symétrie - l'excentricité
 vaut 1 et l'unique foyer
vaut 1 et l'unique foyer  est à la distance
est à la distance 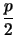 du sommet sur l'axe de symétrie
du sommet sur l'axe de symétrie
C'est : 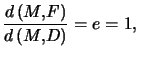 La distance du foyer à la directrice est
La distance du foyer à la directrice est  .
.
On a : 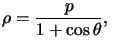 le foyer
le foyer  étant à l'origine.
étant à l'origine.
 est le paramètre de la parabole, distance du foyer à la directrice,
est le paramètre de la parabole, distance du foyer à la directrice, - l'axe de symétrie est
 et contient le foyer.
et contient le foyer.
C'est : 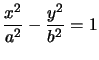
C'est : 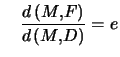 , avec
, avec 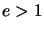 . Les éléments de l'hyperbole sont précisés figure ci-dessous.
. Les éléments de l'hyperbole sont précisés figure ci-dessous.
![\includegraphics[width=6in]{hyperbole}](img1191.png)
C'est : 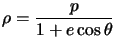 un des foyers
un des foyers  étant à l'origine
étant à l'origine
 est le paramètre de l'hyperbole, distance du foyer à la directrice correspondante,
est le paramètre de l'hyperbole, distance du foyer à la directrice correspondante,  est l'excentricité
est l'excentricité - l'axe focal est

On part d'un polynôme non nul du second degré en  et
et 
- cas où il n'y a pas de termes en

- avaler, si possible, les termes en
 et en
et en  dans des carrés
dans des carrés
Cela revient à faire une translation de l'origine du repère. - se ramener ensuite à une des formes canoniques décrites.
- On trouve des paraboles, hyperboles et ellipses (ou cercles)
- mais aussi des coniques dégénérées : couple de droites, droite, point, vide.
- cas où il y a des termes en

- on repère la forme quadratique formée des seuls termes du second degré :
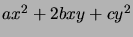 on considère sa matrice
on considère sa matrice ![\begin{displaymath}\left( \begin{array}[c]{cc} a & b\\ b & c \end{array} \right) \quad\end{displaymath}](img1197.png) qu'on diagonalise dans une base orthonormale directe de vecteurs propres, avec
qu'on diagonalise dans une base orthonormale directe de vecteurs propres, avec  la matrice de passage et
la matrice de passage et  et
et  les deux valeurs propres.
les deux valeurs propres.
Cela revient à faire une rotation du repère. - alors
 avec
avec ![\begin{displaymath}\left( \begin{array}[c]{c} x\\ y \end{array} \right) =P\left( \begin{array}[c]{c} X\\ Y \end{array} \right) \quad\end{displaymath}](img1199.png) qui nous sert aussi à transformer le reste de l'équation de la conique.
qui nous sert aussi à transformer le reste de l'équation de la conique. - il n'y a donc plus de termes en
 dans ce repère. On est ramené au cas précédent.
dans ce repère. On est ramené au cas précédent.
© Christophe Caignaert - Lycée Colbert - Tourcoing![]() avec
avec ![]() un polynôme du second degré.
un polynôme du second degré.
![]() est la distance du centre aux foyers
est la distance du centre aux foyers![]() est l'excentricité
est l'excentricité![\includegraphics[width=6in]{ellipse}](img1175.png)
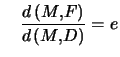 , avec
, avec ![]()
![]() un des foyers
un des foyers ![]() étant à l'origine
étant à l'origine ![]() avec
avec ![]() le paramètre
le paramètre 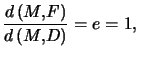 La distance du foyer à la directrice est
La distance du foyer à la directrice est ![]() .
.![]() le foyer
le foyer ![]() étant à l'origine.
étant à l'origine. 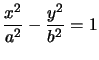
![]() est la distance du centre aux foyers
est la distance du centre aux foyers![]() est l'excentricité
est l'excentricité 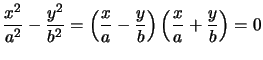
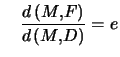 , avec
, avec ![]() . Les éléments de l'hyperbole sont précisés figure ci-dessous.
. Les éléments de l'hyperbole sont précisés figure ci-dessous.![\includegraphics[width=6in]{hyperbole}](img1191.png)
![]() un des foyers
un des foyers ![]() étant à l'origine
étant à l'origine ![]() et
et ![]()

![\begin{displaymath}\left( \begin{array}[c]{cc} a & b\\ b & c \end{array} \right) \quad\end{displaymath}](img1197.png) qu'on diagonalise dans une base orthonormale directe de vecteurs propres, avec
qu'on diagonalise dans une base orthonormale directe de vecteurs propres, avec ![\begin{displaymath}\left( \begin{array}[c]{c} x\\ y \end{array} \right) =P\left( \begin{array}[c]{c} X\\ Y \end{array} \right) \quad\end{displaymath}](img1199.png) qui nous sert aussi à transformer le reste de l'équation de la conique.
qui nous sert aussi à transformer le reste de l'équation de la conique.