Résumé de Cours de Sup et Spé T.S.I.
Troisième Partie : Géométrie
35 Quadriques
Sous-sections
Une quadrique, éventuellement dégénérée, est une surface ayant pour équation cartésienne  avec
avec  un polynôme du second degré.
un polynôme du second degré.
Sur la figure ci-dessous, on a représenté les cinq quadriques propres.
![$\textstyle \parbox{3.2in}{\begin{center} \includegraphics[width=3.2in]{PE} \\ Parabolo\uml {i}de Elliptique \end{center}}$](img1218.png)
![$\textstyle \parbox{3.2in}{\begin{center} \includegraphics[ width=3.2in ] {PH} \\ Parabolo\uml {i}de Hyperbolique \end{center}}$](img1219.png)
![$\textstyle \parbox{3.2in}{\begin{center} \includegraphics[ width=3.2in ] {H1} \\ Hyperbolo\uml {i}de \\lq {a} une nappe \end{center}}$](img1220.png)
![$\textstyle \parbox{3.2in}{\begin{center} \includegraphics[ width=3.2in ] {H2} \\ Hyperbolo\uml {i}de \\lq {a} 2 nappes \end{center}}$](img1221.png)
![$\textstyle \parbox{4in}{\begin{center} \includegraphics[width=4in]{E} \\ Ellipsoïde \end{center}}$](img1222.png)
| E | PE | PH | H1 | H2 |
Ellipse | 
| 
| | 
| 
|
Parabole | | 
| 
| 
| 
|
Hyperbole | | | 
| 
| 
|
Deux droites | | | 
| 
| |
Point | 
| 
| | | 
|
Vide | 
| 
| | | 
|
On part d'un polynôme du second degré en  ,
,  et
et  .
.
- cas où il n'y a de termes ni en
 , ni en
, ni en 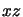 ni en
ni en  ,
, - avaler si possible les termes en
 ,
,  et en
et en  dans des carrés
dans des carrés
Cela revient à faire une translation de l'origine du repère. - se ramener ensuite à une des formes canoniques décrites.
- On trouve des paraboloïdes elliptiques et hyperboliques, hyperboloïdes à 1 ou 2 nappes et ellipsoïdes (ou sphères)
- mais aussi des quadriques dégénérées: cylindres, cônes, ..., point, vide
- cas où il y a des termes en
 ,
, 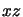 ou
ou  ,
, - la forme quadratique est formée des termes du second degré :
 , on considère sa matrice :
, on considère sa matrice : ![\begin{displaymath}\left( \begin{array}[c]{ccc} a & b & c\\ b & d & e\\ c & e & f \end{array} \right) , \quad\end{displaymath}](img1227.png) qu'on diagonalise dans une base orthonormale de vecteurs propres, avec
qu'on diagonalise dans une base orthonormale de vecteurs propres, avec  la matrice de passage et
la matrice de passage et  ,
,  et
et  , les trois valeurs propres.
, les trois valeurs propres.
Si on a pris une base orthonormale directe, cela revient à faire une rotation du repère. - alors :
 avec
avec ![\begin{displaymath}\left( \begin{array}[c]{c} x\\ y\\ z \end{array} \rig... ...begin{array}[c]{c} X\\ Y\\ Z \end{array} \right) , \quad\end{displaymath}](img1230.png) qui nous sert aussi à transformer le reste de l'équation de la quadrique.
qui nous sert aussi à transformer le reste de l'équation de la quadrique. - il n'y a donc plus de termes en
 ,
, 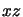 ou
ou  dans ce repère.
dans ce repère.
On est ramené au cas précédent.
© Christophe Caignaert - Lycée Colbert - Tourcoing![]() avec
avec ![]() un polynôme du second degré.
un polynôme du second degré. avec
avec 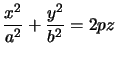 avec
avec  avec
avec  ce qui donne :
ce qui donne : ![\begin{displaymath}\left\{ \begin{array}[c]{l} \dfrac{x}{a}-\dfrac{y}{b}=k\\... ...c{x}{a}+\dfrac{y}{b}=\dfrac{2pz}{k} \end{array} \right. \quad\end{displaymath}](img1209.png) et :
et : ![\begin{displaymath}\left\{ \begin{array}[c]{l} \dfrac{x}{a}+\dfrac{y}{b}=k\\... ...c{x}{a}-\dfrac{y}{b}=\dfrac{2pz}{k} \end{array} \right. \quad\end{displaymath}](img1210.png) avec
avec  avec
avec 
 , et
, et 
![\begin{displaymath}\left\{ \begin{array}[c]{l} \dfrac{x}{a}-\dfrac{z}{c}=k\lef... ...c{1}{k}\left( 1+\dfrac{y}{b}\right) \end{array} \right. \quad\end{displaymath}](img1215.png) et :
et : ![\begin{displaymath}\left\{ \begin{array}[c]{l} \dfrac{x}{a}+\dfrac{z}{c}=k\lef... ...c{1}{k}\left( 1+\dfrac{y}{b}\right) \end{array} \right. \quad\end{displaymath}](img1216.png) avec
avec  avec
avec 
![$\textstyle \parbox{3.2in}{\begin{center} \includegraphics[width=3.2in]{PE} \\ Parabolo\uml {i}de Elliptique \end{center}}$](img1218.png)
![$\textstyle \parbox{3.2in}{\begin{center} \includegraphics[ width=3.2in ] {PH} \\ Parabolo\uml {i}de Hyperbolique \end{center}}$](img1219.png)
![$\textstyle \parbox{3.2in}{\begin{center} \includegraphics[ width=3.2in ] {H1} \\ Hyperbolo\uml {i}de \\lq {a} une nappe \end{center}}$](img1220.png)
![$\textstyle \parbox{3.2in}{\begin{center} \includegraphics[ width=3.2in ] {H2} \\ Hyperbolo\uml {i}de \\lq {a} 2 nappes \end{center}}$](img1221.png)
![$\textstyle \parbox{4in}{\begin{center} \includegraphics[width=4in]{E} \\ Ellipsoïde \end{center}}$](img1222.png)
![]() ,
, ![]() et
et ![]() .
. 
![\begin{displaymath}\left( \begin{array}[c]{ccc} a & b & c\\ b & d & e\\ c & e & f \end{array} \right) , \quad\end{displaymath}](img1227.png) qu'on diagonalise dans une base orthonormale de vecteurs propres, avec
qu'on diagonalise dans une base orthonormale de vecteurs propres, avec ![\begin{displaymath}\left( \begin{array}[c]{c} x\\ y\\ z \end{array} \rig... ...begin{array}[c]{c} X\\ Y\\ Z \end{array} \right) , \quad\end{displaymath}](img1230.png) qui nous sert aussi à transformer le reste de l'équation de la quadrique.
qui nous sert aussi à transformer le reste de l'équation de la quadrique.