Résumé de Cours de Sup et Spé T.S.I.

Quatrième Partie : Maple

42 Exemples de Programmes

Sous-sections

42 Exemples de Programmes

Remarque : Notons qu'aucun des programmes donnés ici en exemple n'est « protégé » contre une mauvaise utilisation avec des paramètres non pertinents...

42.1 Un programme très simple

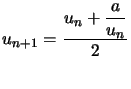On va maintenant créer une procédure qui calcule, pour un terme donné , le terme suivant de la suite $u_{n+1}$ défini par : $u_{n+1}=\dfrac{u_{n}+\displaystyle\frac{a}{u_{n}}}{2}$ .
On a donc deux paramètres : le terme donné de la suite, appelé dans la procédure, et .

$\fbox{\begin{minipage}{17cm} \begin{gather*} \mathit{suivant} := \textbf{proc}... ...\ast a / v\,;\\ \quad v\\ \textbf{end proc} \end{gather*} \end{minipage}}$

42.2 Structure alternative

On va écrire une procédure qui calcule, pour une expression usuelle du second degré $ax^{2}+bx+c$ à coefficients réels, le nombre de ses racines réelles.
On a donc trois paramètres .

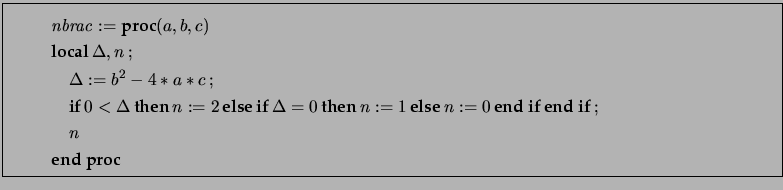
$\fbox{\begin{minipage}{17cm} \begin{gather*} \mathit{nbrac} := \textbf{proc} (... ...{end if} \,;\\ \quad n \\ \textbf{end proc} \end{gather*} \end{minipage}}$

42.3 Structure itérative « pour » à nombre de pas connu

Ecrivons une procédure qui, pour la même suite qu'au 42.1, calcule, en calcul approché « flottant », pour, et paramètres donnés, que dans la procédure, on appelera respactivement :.

$\fbox{\begin{minipage}{17cm} \begin{gather*} \mathit{suitef} := \textbf{proc} ... ...{end do} \,;\\ \quad v \\ \textbf{end proc} \end{gather*} \end{minipage}}$

42.4 Structure itérative « tant que » à nombre de pas inconnu

Il s'agit ici d'étudier le comportement des suites définies par :

$u_{0}=0.1$ ,
et la relation de récurrence : $u_{n+1}=f\left( u_{n}\right)$ ,
où $f(x)=4\,a\,x(1-x)$ .

Ecrire une procédure de paramètres et qui calcule $u_{n}$ .

$\fbox{\begin{minipage}{17cm} \begin{gather*} \mathit{suite} := \textbf{proc} (... ...f{end do} \,;\\ \quad u\\ \textbf{end proc} \end{gather*} \end{minipage}}$

Ecrire maintenant une procédure qui calcule le premier tel que $\left\vert u_{n+1}-u_{n}\right\vert \leqslant d$ , de paramètres et , limitée à 500 itérations en cas de divergence ou de convergence très lente ... En sortie, on donnera $n,u_{n},u_{n+1}$ pour voir s'il semble y avoir convergence ou non.
Mathématiquement, l'observation de ces suites ne prouve ni leur convergence, ni leur divergence.

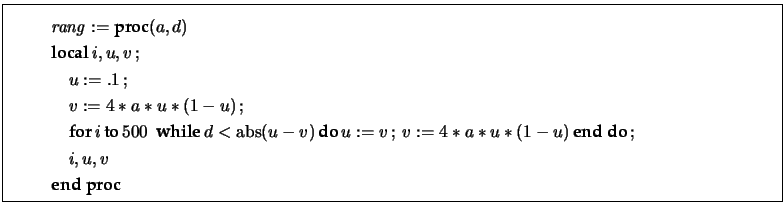
$\fbox{\begin{minipage}{17cm} \begin{gather*} \mathit{rang} := \textbf{proc} (a... ...,; \\ \quad i, \,u, \,v \\ \textbf{end proc} \end{gather*} \end{minipage}}$

42.5 Récurrence sur plusieurs rangs

On considère la suite de polynômes définie par :

$P_{0}(x)=1$

$P_{1}(x)=x$

$P_{n+2}(x)=x\,P_{n+1}(x)+P_{n}(x)$ pour entier naturel

Ecrire une procédure de paramètre , qui calcule de façon réduite et ordonnée $P_{n}$ .

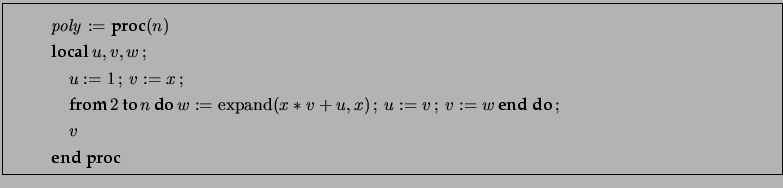
$\fbox{\begin{minipage}{17cm} \begin{gather*} \mathit{poly} := \textbf{proc} (n... ...f{end do} \,;\\ \quad v \\ \textbf{end proc} \end{gather*} \end{minipage}}$

On remarquera le « from 2 » qui traduit simplement le fait que le premier polynôme qu'on calcule effectivement est .

42.6 Un exemple en algèbre linéaire

On a bien sur déjà chargé le package linalg. On prend ici une matrice qui possède 3 valeurs propres simples : 1, 4 et 7.
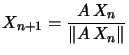On constitue la suite de vecteurs définie par un pemier vecteur et la relation : $X_{n+1}=\dfrac{A\,X_n}{\left\Vert A\,X_n\right\Vert}$ .
On a donc une suite de vecteurs normés, sauf éventuellement le premier.
Quand cette suite converge, elle converge vers un vecteur propre, correspondant le plus souvent à la plus grande valeur propre en valeur absolue.
On a la matrice et le vecteur de départ :

$\fbox{\begin{minipage}{17cm} \begin{gather*} A := \left[ \begin{array}{rrr}... ...3 \end{array} \right] \\ X := [1, \,1, \,1] \end{gather*} \end{minipage}}$

On écrit donc une procédure à 2 paramètres et qui calcule la suite jusqu'à ce que la norme de la différence de 2 vecteurs consécutifs soit assez petite.
Le nombre d'itérations est limité et on travaille bien sûr en « flottant ».
Ce qui donne :

$\fbox{\begin{minipage}{17cm} \begin{gather*} \mathit{valprop} := \textbf{proc}... ...m{\lq \&*\lq }(A, \,Z)), \,2)) \\ \textbf{end proc} \end{gather*} \end{minipage}}$

On essaye cette procédure :

$\fbox{\begin{minipage}{17cm} \begin{gather*} \mathrm{> \; valprop(A,X);}\\ \\ \qquad 6.999999999 \end{gather*} \end{minipage}}$