Résumé de Cours de Sup et Spé T.S.I.

Première Partie : Algèbre

4 Polynômes

Sous-sections

4 Polynômes


4.1 Racines

Soit le polynôme : 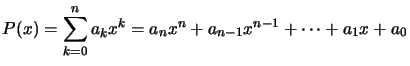   $ P(x)=\displaystyle\sum_{k=0}^{n}a_{k}x^{k}=a_{n}x^{n}+a_{n-1}x^{n-1}+\cdots+a_{1}x+a_{0} $

Théorème :   Sur $ \mathbb{C}$,    $ P(x)=a_{n}\left( x-x_{1}\right) \left( x-x_{2}\right) \cdots\left( x-x_{n}\right) $

Théorème :   Sur $ \mathbb{R}$,    $ P(x)=a_{n}\left( x-x_{1}\right) \left( x-x_{2}\right) \cdots\left( x-x_{p}\ri... ...+\alpha_{1}x+\beta_{1}\right) \cdots\left( x^{2}+\alpha_{m}x+\beta_{m}\right) $ avec $ p+2m=n$ et toutes les expressions du second degré irréductibles, c'est à dire $ \Delta<0$.

Remarque :   Quand on a tous les facteurs d'un polynôme, pour retrouver celui-ci, il ne faut pas oublier le coefficient dominant $ a_{n}$.

Définition :   Un polynôme est dit scindé si et seulement si il est factorisable en produit d'expressions du premier degré.

Sur $ \mathbb{C}$ un polynôme est donc toujours scindé. Sur$ \mathbb{R}$, il faut et il suffit qu'il n'ait pas de racines complexes non réelles.

Théorème :   $ P(x)$ est divisible par $ \left( x-\alpha\right) \Leftrightarrow P(\alpha)=0\Leftrightarrow\alpha$ est racine de $ P$

Théorème :   $ P(x)$ est divisible par $ \left( x-\alpha\right) ^{k}\Leftrightarrow P(\alpha)=P^{\prime}(\alpha)=\cdots=P^{(k-1)}(\alpha)=0$$ \Leftrightarrow\alpha$ est racine d'ordre $ k$ au moins de $ P$

Théorème :   Un polynôme de degré $ n$ qui a au moins $ n+1$ racines distinctes ou confondues est nul.

Théorème :   Si P est scindé,    $ x_{1}+x_{2}+\cdots+x_{n}=-\dfrac{a_{n-1}}{a_{n}} $,    $ \ x_{1}x_{2}\ldots x_{n}=\left( -1\right) ^{n}\dfrac{a_{0}}{a_{n}}$

Remarque :   Pour le degré 2,    $ x^{2}-Sx+P=0$    est tel que :     $ S=x_{1}+x_{2}$, et $ \ P=x_{1}\, x_{2}$$ S$ est la somme des racines et $ P$ leur produit.


4.2 Division Euclidienne

Théorème :   Soit A et B deux polynômes, $ B\neq0$$ ,\ $ alors il existe un unique couple $ \left( Q,R\right) $ tel que \begin{displaymath}\left\{ \begin{array}[c]{l} A=B\, Q+R\\ \mathrm{degr\acute{e}}(R)<\mathrm{degr\acute{e}}(B) \end{array} \right. \end{displaymath}

En pratique, quand on écrit la division de $ A$ par $ B$, on prendra soin de bien écrire les polynômes par puissances décroissantes.

Remarque :   $ P\vert Q \Leftrightarrow$ Le reste de la division euclidienne de $ Q$ par $ P$ est nul    
 $ \Leftrightarrow$ Toutes les racines de $ P$ sont racines de $ Q$ avec au moins le même ordre de multiplicité.
On pensera à cette dernière équivalence quand le degré de $ P$ est petit ...


© Christophe Caignaert - Lycée Colbert - Tourcoing