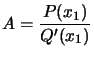Théorème : 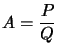 une fraction rationelle irréductible avec
une fraction rationelle irréductible avec ![]()
Alors : 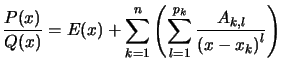 avec
avec ![]() le quotient de la division euclidienne de
le quotient de la division euclidienne de ![]() par
par ![]() .
.
En pratique, sur les réels et les complexes,
 ,
, 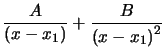 (première espèce).
(première espèce).Sur les réels,
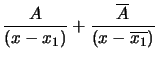
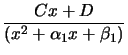 (seconde espèce), avec
(seconde espèce), avec Exemple : On va donner un exemple de décomposition directe en éléments simples sur ![]() .
.
Soit : 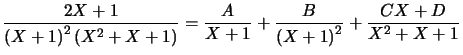 car
car ![]() n'a pas de racines réelles, ses racines sont
n'a pas de racines réelles, ses racines sont ![]() et
et ![]() .
.
Pour ![]() , on multiple par
, on multiple par ![]() , on simplifie et on fait
, on simplifie et on fait![]() .
.
Cela donne : ![]() .
.
Pour ![]() et
et ![]() , qu'on peut trouver en même temps, car la fraction rationelle du départ est réelle, on multiplie par
, qu'on peut trouver en même temps, car la fraction rationelle du départ est réelle, on multiplie par ![]() , on simplifie et on fait
, on simplifie et on fait ![]() .
.
Comme ![]() et
et ![]() sont réels, on a les deux.
sont réels, on a les deux.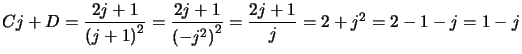 , d'où :
, d'où : ![]() et
et ![]() .
.
Pour ![]() , on fait
, on fait ![]() ou bien on multiplie par
ou bien on multiplie par ![]() et on fait
et on fait ![]() .
.
Ce qui donne : ![]() et donc :
et donc : ![]() .
.
Pour décomposer une fraction rationelle en éléments simples, il faut :