Résumé de Cours de Sup et Spé T.S.I.

Première Partie : Algèbre

8 Matrices

Sous-sections

8 Matrices

8.1 Généralités

8.1.1 Matrices symétriques et antisymétriques

Définition : Une matrice carré est symétrique $\Leftrightarrow \,^tM=M\Leftrightarrow a_{ji}=a_{ij}$

Définition : Une matrice carré est anti-symétrique $\Leftrightarrow \,^tM=-M\Leftrightarrow a_{ji}=-a_{ij}$

Théorème : Le sous-espace vectoriel des matrices symétriques et le sous-espace vectoriel des matrices antisymétriques sont supplémentaires.
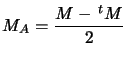
De plus : $M_S=\dfrac{M+\,^tM}{2}$ et $M_A=\dfrac{M-\,^tM}{2}$

8.1.2 Produit de matrices

Si est une matrice -lignes et -colonnes, une matrice -lignes et -colonnes, alors : est une matrice -lignes et -colonnes vérifiant : $c_{ij}=\displaystyle\sum_{k=1}^ma_{ik}\,b_{kj}$ .
Ce qui se schématise : $\begin{displaymath}\left( \begin{array}[c]{ccc} \cdots & \cdots & \cdots \\... ...\cdots & c_{ij} & \cdots \\ & \vdots & \end{array} \right) \end{displaymath}$

8.1.3 Produit de matrices définies par blocs

Si deux matrices sont définies par blocs, on peut parfois effectuer leur produit en travaillant par blocs.
C'est à dire :

$\displaystyle \left(\begin{array}[c]{cc} (A) & (B)\\ (C) & (D) \end{array} ... ...imes (A')+(D)\times (C') & (C)\times (B')+(D)\times (D') \end{array} \right)$

Remarque : Les dimensions des matrices doivent être compatibles, à savoir :

Le nombre de colonnes de et doit être le nombre de lignes de et .
Le nombre de colonnes de et doit être le nombre de lignes de et .

D'autre part, rappelons que le produit de matrices n'est pas commutatif, l'ordre dans lequel on écrit ces produits est donc fondamental...

8.1.4 Transposée d'un produit

Théorème : On a : $^{t}\!(AB)=\,^{t}\!B\,^{t}\!\!A$

8.2 Généralités sur les matrices carrées

8.2.1 Inverse d'une matrice

Théorème : Si on a une matrice carrée telle que : $M\,M'=I_n$ , ou telle que : $M'\,M=I_n$ , alors est inversible et $M^{-1}=M'$ .

Théorème : Une matrice carrée est inversible si et seulement si son déterminant est non nul.

En général, on inverse une matrice carrée en inversant le système linéaire correspondant avec un second membre arbitraire : $Y=MX\Leftrightarrow X=M^{-1}Y$
Cependant, parfois, quand la question est plus théorique, on peut utiliser le théorème suivant :

Théorème : , une matrice inversible, $\Delta$ son déterminant et $\Delta_{ij}$ le déterminant obtenu en enlevant la $i^{\grave{e}me}$ ligne et la $j^{\grave{e}me}$ colonne, alors :

$\displaystyle M^{-1}=\dfrac{1}{\Delta }\times$ transposée de $\begin{displaymath} \left( \begin{array}[c]{ccc} & \vdots & \\ \cdots & (-... ...\,\Delta_{ij} & \cdots \\ & \vdots & \end{array} \right) \end{displaymath}$

8.2.2 Inverse d'un produit

Théorème : On a : $(AB)^{-1}=B^{-1}A^{-1}$

8.3 Matrice d'une application linéaire

Définition : $f:E\rightarrow F$ , linéaire, avec E et F de dimensions finies et , munis de bases $\mathcal{B}_{E}=(e_{1},\ldots,\, e_{n})$ et $\mathcal{B} _{F}=(e_{1}^{\prime},\ldots,\, e_{p}^{\prime})$ , on appelle matrice de f dans ces bases $\mathcal{M}_{\mathcal{B}_{E},\mathcal{B}_{F}}$ la matrice lignes et colonnes dont l'élément $a_{i,j}$ , $i^{\grave{e} me}\text{ ligne et }j^{\grave{e}me}\text{ colonne}$ est tel que $f(e_{j})=\displaystyle\sum_{i=1}^{p}a_{i,j}\, e_{i}^{\prime}$ .

On a en colonnes, les coordonnées des images des vecteurs de la base de écrits dans la base de .

$\begin{displaymath} \begin{array}[c]{cc} \left( \begin{array}[c]{ccccc} a_{1... ... f( e_{j}) & \ldots & f( e_{n}) \end{array} & \end{array} \end{displaymath}$

8.4 Matrice de Passage

Définition : On appelle matrice de passage ou P $_{\mathcal{B}_{1}\mathcal{B}_{2}}$ la matrice constituée en colonnes des coordonnées des vecteurs de la nouvelle base $\mathcal{B}_{2}$ écrits dans l'ancienne $\mathcal{B}_{1}$ .
On l'appelle aussi matrice de changement de base.

C'est donc une matrice inversible.
Toute matrice carrée inversible peut toujours s'interpréter

comme matrice d'un endomorphisme dans une certaine base,
ou comme matrice de changement de base.

Passer d'une interprétation à une autre permet parfois de faire avancer le problème.

8.5 Changements de base

Théorème : Si on appelle et $X^{\prime}$ les vecteurs colonnes, coordonnées d'un vecteur dans l'ancienne et la nouvelle base, et P la matrice de passage, on a $X=PX^{\prime}$ ou bien $X^{\prime}=P^{-1}X$ .

Théorème : Si on appelle et $M^{\prime}$ les matrices d'un endomorphisme dans l'ancienne et la nouvelle base, et P la matrice de passage, on a $M^{\prime }=P^{-1}MP$ ou bien $M=PM^{\prime}P^{-1}$ .

Définition : M et M' sont semblables $\Leftrightarrow\exists P$ inversible telle que $M^{\prime }=P^{-1}MP$ $\Leftrightarrow$ ce sont les matrices d'un même endomorphisme dans deux bases différentes.