Résumé de Cours de Sup et Spé T.S.I.

Première Partie : Algèbre

11 Espaces Préhilbertiens Réels et Euclidiens

Sous-sections

11 Espaces Préhilbertiens Réels et Euclidiens

11.1 Produit scalaire

Définition : Soit un espace vectoriel sur $\mathbb{R}$ , une forme bilinéaire symétrique sur est une application de $E\times E\rightarrow\mathbb{R}$

linéaire par rapport à chacune des variables (l'autre étant fixée) et
symétrique (on peut inverser l'ordre des variables).

Définition : Une forme quadratique sur $\mathbb{R}^n$ est une application de $\mathbb{R}^n\rightarrow\mathbb{R}$ qui se met sous la forme d'un polynôme homogène de degré 2 des coordonnées du vecteur de $\mathbb{R}^n$ .

Théorème : Si $\varphi$ est une forme bilinéaire symétrique sur , alors : $q:\left\{ \begin{array}[c]{l} E\rightarrow\mathbb{R}\\ u\mapsto q\left( u\right) =\varphi\left( u,u\right) \end{array} \right.$ est une forme quadratique, appelée forme quadratique associée à $\varphi$ .
Par ailleurs, si est une forme quadratique sur , alors $\varphi : E\times E\rightarrow\mathbb{R}$ définie par :

$\displaystyle \varphi\left( u,v\right) =\dfrac{q\left( u+v\right) -q\left( u\right) -q\left( v\right) }{2}$

est une forme bilinéaire symétrique. C'est la forme polaire de .

Définition : E un espace vectoriel réel. Un produit scalaire est une application de $E\times E\rightarrow\mathbb{R}$ bilinéaire, symétrique, définie-positive.

En pratique, on montre :

$\forall u,v\in E,\quad\left\langle u,v\right\rangle =\left\langle v,u\right\rangle$ . La forme est symétrique

$\begin{displaymath}\left. \begin{array}[c]{r} \forall u_{1},\, u_{2},\, v\in E... ...},\, v\right\rangle +\mu\left\langle u_{2} ,\, v\right\rangle \end{displaymath}$ . La forme est donc bilinéaire symétrique

$\forall u,\in E,\quad\left\langle u,u\right\rangle \geqslant0$ . La forme est positive

$\left\langle u,u\right\rangle =0\Rightarrow u=0$ . La forme est définie-positive

C'est souvent le dernier point qui pose problème.

Remarque : Quand le produit scalaire est défini par une intégrale, c'est à ce moment qu'on utilise le théorème des 3 conditions.

Théorème : E étant muni d'une base $(e_{1},\ldots,\, e_{n})$ ,
On note : $\begin{displaymath}U:\left( \begin{array}[c]{c} x_{1}\\ x_{2}\\ \vdots\\ x_{n} \end{array} \right) \end{displaymath}$ et $\begin{displaymath}V:\left( \begin{array}[c]{c} y_{1}\\ y_{2}\\ \vdots\\ y_{n} \end{array} \right) \end{displaymath}$ les vecteurs colonnes des coordonnées de et dans la base,
On note , la matrice symétrique où $a_{i,j}=\left\langle e_{i},e_{j}\right\rangle$ , alors :

$\displaystyle \left\langle u,v\right\rangle =\; ^{t}U\! AV$

est ainsi la matrice de la forme bilinéaire symetrique, encore appelée matrice du produit scalaire dans la base $(e_{1},\ldots,\, e_{n})$ .
Si, de plus, la base est orthonormale, alors on a :

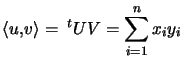
$\displaystyle \left\langle u,v\right\rangle =\ ^{t} UV=\displaystyle\sum_{i=1}^{n}x_{i}y_{i}$

Définition : La norme euclidienne est : $\left\Vert u\right\Vert =\sqrt{\left\langle u,u\right\rangle }=\sqrt{\displaystyle\sum_{i=1}^{n}x_{i}^{2}}$

Exemple : Sur les matrices carrées, le produit scalaire usuel est : $\left\langle A,B\right\rangle =\mathrm{trace}(\,^t\! AB)= \displaystyle\sum_{i=1}^n\displaystyle\sum_{i=1}^n a_{i,j}\, b_{i,j}$

11.2 Espaces vectoriels préhilbertiens et euclidiens

Définition : E un espace vectoriel réel est dit préhilbertien réel quand il est muni d'un produit scalaire.
Si, de plus, il est de dimension finie, il est dit euclidien.

11.3 Inégalités

Théorème : On a l'inégalité de Schwarz : $\forall u,v\in E$ , $\left\vert \left\langle u,v\right\rangle \right\vert \leqslant\left\Vert u\right\Vert \left\Vert v\right\Vert$ .

Théorème : On a l'inégalité triangulaire : $\forall u,v\in E$ , $\left\Vert u+v\right\Vert \leqslant\left\Vert u\right\Vert +\left\Vert v\right\Vert$ .

11.4 Endomorphismes symétriques

Définition : Un endomorphisme est dit symétrique $\Leftrightarrow\forall u,v\in E,\quad\left\langle f(u),v\right\rangle =\left\langle v,f(u)\right\rangle$

Théorème : est symétrique $\Leftrightarrow$ sa matrice dans une base orthonormale est symétrique.

11.5 Matrice symétrique réelle

Théorème : Une matrice symétrique réelle est diagonalisable dans une base orthonormale, c'est à dire avec au besoin une matrice de passage orthogonale, telle que : $P^{-1}=$ $^{t}P$ .
Les sous-espaces propres ainsi que les vecteurs propres associés à des valeurs propres distinctes sont orthogonaux 2 à 2.

11.6 Procédé de Schmidt

Théorème : Tout espace vectoriel euclidien possède une base orthonormale.

Le procédé de Schmidt permet de construire effectivement une base orthonormale à partir d'une base quelconque.

On part d'une base quelconque $\left( e_{1},\, e_{2},\ldots,\, e_{n}\right)$
On pose $\varepsilon_{1}=\dfrac{e_{1}}{\left\Vert e_{1}\right\Vert }$ C'est le premier vecteur de la base orthonormale.
On pose $\varepsilon_{2}^{\ast}=e_{2}+\lambda.\varepsilon_{1}$ On cherche $\lambda$ tel que $\left\langle \varepsilon_{2}^{\ast},\, \varepsilon _{1}\right\rangle =0$ , ce qui donne : $\lambda=-\left\langle e_{2} ,\, \varepsilon_{1}\right\rangle$
On pose $\varepsilon_{2}=\dfrac{\varepsilon_{2}^{\ast}}{\left\Vert \varepsilon_{2}^{\ast}\right\Vert }$ C'est le deuxième vecteur de la base orthonormale.
On pose $\varepsilon_{3}^{\ast}=e_{3}+\lambda.\varepsilon_{1} +\mu.\varepsilon_{2}$ On cherche $\lambda$ et $\mu$ tel que $\begin{displaymath}\left\{ \begin{array}[c]{l} \left\langle \varepsilon_{3}^{\... ...{\ast},\,\varepsilon_{2}\right\rangle =0 \end{array} \right. \end{displaymath}$ , d'où : $\begin{displaymath}\left\{ \begin{array}[c]{l} \lambda=-\left\langle e_{3},\,\... ...gle e_{3},\,\varepsilon_{2}\right\rangle \end{array} \right. \end{displaymath}$
On pose $\varepsilon_{3}=\dfrac{\varepsilon_{3}^{\ast}}{\left\Vert \varepsilon_{3}^{\ast}\right\Vert }$ C'est le troisième vecteur de la base orthonormale.
On continue ainsi en n'oubliant pas que chaque étape s'allonge...

11.7 Projection orthogonale sur un sous espace de dimension finie

Théorème : un espace vectoriel préhilbertien, un sous espace vectoriel de dimension finie muni d'une base orthonormale $\left( e_{1},\, e_{2},\ldots,\, e_{n}\right)$ .
Alors

$\displaystyle p:u\rightarrow p\left( u\right) =\left\langle u,\, e_{1}\right\rangle .e_{1}+\cdots+\left\langle u,\, e_{n}\right\rangle .e_{n}$

définit un projecteur. Et comme $\left( u-p\left( u\right) \right) \in F^{\perp}$ , on dit que est la projection orthogonale sur .

Ce qu'on peut voir sur la figure ci-dessous.

$\includegraphics[width=4.8in]{Proj-sev-dim-finie}$